|
-
Le segment utilisateur
Physiquement, le segment utilisateur se compose d’une antenne de réception des signaux satellites, voire ceux émis par les stations terrestres. C’est le récepteur qui effectue les calculs de coordonnées à partir des informations reçues des satellites.
I) Positionnement absolu
Pour déterminer les coordonnées sphériques de l’utilisateur, c'est-à-dire dans un repère géocentrique théorique, GPS comme GLONASS ou le système GALILEO à venir, tous utilisent un principe fondamental similaire, basé sur la résolution de simples systèmes d’équations. Cette technique de recherche d’intersections multiples peut être appelée la triangulation, dès lors qu’il y a trois équations dans le système. Mais la précision est d’autant plus grande qu’il y a plus de signaux reçus. Ainsi, il s’agit souvent de tétralation, de pentalation, de sextulation, d’heptalation, d’octalation, d’ennéalation, de décalation, d’endécalation, voire dans le meilleur des cas de dodécalation… Nous étudierons spécifiquement le principe de triangulation, puisque les niveaux supérieurs en dérivent et sont tout de même moins fréquents.
1ère phase : émission
Tous les satellites possèdent une horloge atomique qui permet une mesure du temps très précise, ils peuvent donc envoyer sous formes d’ondes radio l’heure précise d’envoi d’un code, à intervalles très rapprochés et dans toutes les directions de l’espace. Les signaux des satellites GPS sont toutefois émis sous deux fréquences distinctes : L1 à 1575 MHz et L2 à 1227 MHz. La deuxième est la plus riche en informations (voir tableau précédent), mais cryptée, elle est réservée aux usagers autorisés de l’armée américaine. |
 |
| |
2ème phase : propagation
Les signaux transmis traversent les 20180 km séparant le satellite du sol terrestre, et leur intégrité est notamment perturbée par les variations d’isotropies de l’atmosphère (cf. la section consacrée au segment de contrôle).
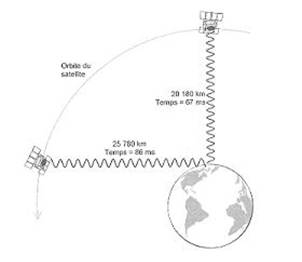
Propagation du signal émis par deux satellites |
3ème phase : réception
Un récepteur reçoit les signaux : c’est à partir de ce moment que commencent les calculs de position. Connaissant l’heure d'émission par le satellite des paquets informatiques reçus et leur heure d'arrivée au récepteur, la distance parcourue se déduit aisément :
Distance = Vitesse de la lumière x (heure d'émission - heure de réception)
Et donc plus formellement : D=cDt
Le repère étant spatial, on obtient le lieu du récepteur sur une sphère ayant pour centre le satellite et pour rayon la distance récepteur/satellite que l'on vient de calculer :

Si ce même récepteur capte le signal d’un second satellite, un calcul équivalent permet de définir une seconde sphère, centrée sur ce second satellite, sur laquelle doit également se trouver notre récepteur. Il se situe alors à la fois sur la première sphère et sur la deuxième. Il est donc quelque part sur le cercle de leur intersection.
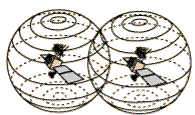
Même chose avec un troisième satellite. Alors, où sommes-nous ? Tout simplement sur l’un des deux points d'intersection de ces trois sphères !
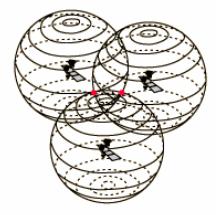
Or, l’utilisateur ne flottant pas dans l’espace, on peut déduire sa position exacte en éliminant le point incohérent.

|
Si les positions des satellites sur leurs orbites sont connues avec suffisamment de précision - ce qui est le cas - et si un récepteur capte au moins 3 satellites, il dispose donc en théorie de trois données qui lui permettent de résoudre les trois inconnues définissant sa position : la latitude, la longitude et l'altitude.
On note R1, R2 et R3 les distances du récepteur par rapport à trois satellites de coordonnées connues (xi, yi, zi). Si (x, y, z) sont les coordonnées de l'utilisateur, la résolution du système suivant permet de déterminer les coordonnées effectives de l'utilisateur dans un repère ECEF (Earth-Centered, Earth-Fixed : Terre-Centré, Terre-Fixé) :

|
| |
Un quatrième satellite est nécessaire
Pour valider tout le raisonnement qui précède, il faudrait que la mesure du temps soit extrêmement précise. Une erreur d’un millième de seconde provoque en effet une erreur de position de 300km ! A la vitesse de la lumière, une très grande précision est de rigueur.
Si les horloges atomiques des satellites sont très précises, et synchronisées au Temps Universel Coordonné UTC via l'observatoire américain USNO exploité par le segment de contrôle, ce n’est pas le cas en revanche des horloges des récepteurs, généralement à quartz. De plus, la transmission des signaux peut être perturbée par de multiples facteurs, que nous détaillerons plus loin.
Il importe donc d’utiliser un 4ème satellite pour rectifier les calculs de manière satisfaisante. Afin de comprendre l'intérêt qu'il constitue (sa présence est prévue dans le cahier des charges de la constellation GPS, GLONASS et GALILEO), ramenons nous à un espace à 2 dimensions, c'est-à-dire un plan.
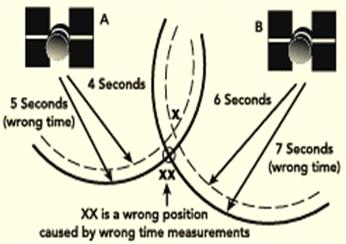
1. En 2D, il faudrait 2 satellites pour repérer un point
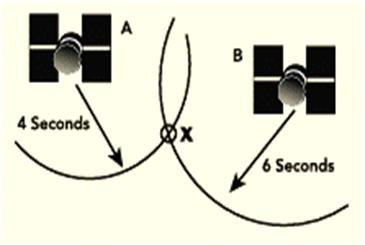
2. Mais si la mesure a une seconde d'erreur, c’est le point XX qui est calculé au lieu du point exact X.
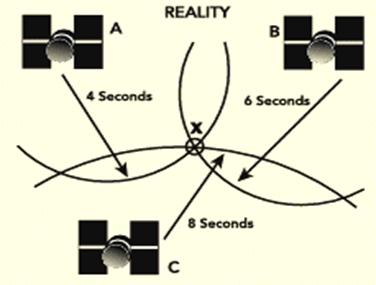
3. L’utilisation d’un troisième satellite sans erreur de mesure lève directement le doute...
4. Dans la pratique, le troisième satellite commet également une erreur du même ordre (1s). Cela permet toutefois de déterminer une zone très restreinte du lieu où se trouve le récepteur.
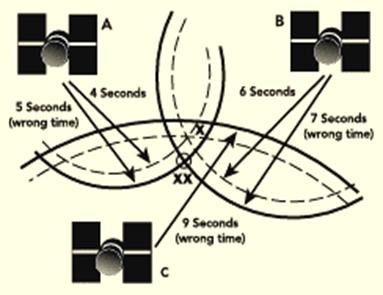
Pour affiner la précision, on peut considérer que l’erreur commise par chacun des satellites A, B et C est la même. Il suffit alors d’enlever à chaque mesure une valeur qui correspond à l’erreur commise pour que les arcs de cercle se coupent en un même point.
Le raisonnement dans la dimension supérieure est identique, il faut simplement recourir à un quatrième satellite. Au final, on dispose donc d’un système de quatre équations à quatre inconnues, qui peut bien sûr être complémenté par les données bienvenues de satellites supplémentaires. La page disponible ici explicite une résolution de coordonnées globales avec le logiciel Mathematica ©. |
II) Mesures de positionnement avancées
Parfois, le positionnement absolu dans le repère ECEF n’est pas assez précis pour l’utilisation souhaitée… Il existe d’autres méthodes de repérage moins directes mais plus avancées qui permettent de fournir des indications de l’ordre de l’infiniment petit à l’échelle de l’espace (le mm par exemple) ! Il s’agit pour la plupart de réduire l’influence des facteurs d’erreurs ou de corriger les calculs en fonction de leurs effets modélisables.
a) Le GPS différentiel
En navigation routière, il ne s’agit pas de conduire les yeux rivés sur son GPS... Mais lors d’un atterrissage par temps de brouillard, un gros porteur aérien comme le très attendu A380 ne peut se permettre d’atterrir à 50 mètres de la piste ! Le besoin d’une précision de l’ordre du mètre se fait donc sentir pour certaines utilisations. Sans requérir plus que les signaux de fréquence L1, la mesure GPS différentielle (DGPS) parvient à cette précision en utilisant des informations radios émises par des stations terrestres de référence.
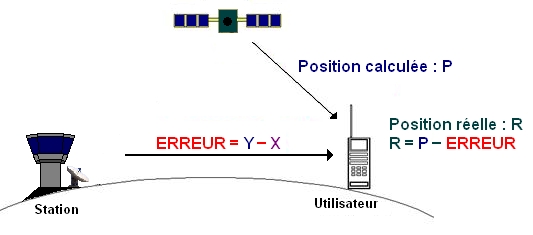
On part en effet du principe que les erreurs volontaires et naturelles sont fortement corrélées, et que par conséquent deux récepteurs géographiquement proches l'un de l'autre réceptionneront des signaux pareillement erronés. Il suffit donc de disposer d’une station de référence (par exemple une tour de contrôle) qui connaît ses coordonnées exactes tout en recevant en permanence les signaux des satellites GPS présent dans son champ de vision. La différence entre ses coordonnées exactes et celles obtenues à l’aide des signaux peut être assimilée à l'erreur commise. Un utilisateur (par exemple un avion) qui dispose d’un récepteur adapté peut alors connaître l’erreur qu’il lui suffit de retrancher en temps réel à ses coordonnées obtenues par GPS pour disposer d'une mesure de positionnement affinée. Le processus en deux étapes peut être schématisé ainsi :
|
Et finalement |
 |
Utilisée très couramment en navigation maritime, la précision DGPS est suffisante pour rentrer au port les yeux fermés (en se laissant guider par la voix du logiciel d’interprétation des données et en écoutant tout de même les alertes radar d’autres navires susceptibles d’être croisés… :-)
Toutefois, les informations apportées par les stations de référence ne sont valables que dans un rayon de moins de 100 km. Au-delà, les différences latérales de l'atmosphère terrestre devenant trop importantes, le signal n’est plus pertinent.
Pour des applications encore plus précises, on peut exploiter directement la phase sur les ondes porteuses L1 ou L2 (si cette dernière réservée au PPS est connue) en déterminant le déphasage entre le satellite et le récepteur. Le récepteur compare en fait la phase du signal reçu avec une phase du même signal qu’il génère lui-même. La distance d’erreur s’obtient alors en multipliant la mesure effectuée par la longueur d'onde l initiale des ondes porteuses qui est connue (l=c/F).
Ce procédé est toutefois plus compliqué que celui basé sur le code (DGPS) car il requiert un récepteur spécifique permettant d'exploiter la phase et capable de réaliser des calculs complexes à l’aide de longs algorithmes. C’est pour cette raison que le traitement des données se fait généralement en mode postopératoire, bien qu’il soit toujours possible de traiter ces signaux en temps réel à condition de disposer de matériel très performant : on parle alors de RTK (Real Time Kinematic).
c) La correction Mayer-Doppler
Si le récepteur est à même de détecter l’arrivée d’un signal de L2 émis en même temps que celui de la fréquence porteuse L1, les lois de Doppler peuvent être utilisées pour mesurer l’erreur résultant de la traversée atmosphérique. En effet, Les ondes L1 et L2 se déplacent à la vitesse de la lumière jusqu’à ce que la traversée des milieux aériens dispersifs réduise leur vitesse en fonction de leur fréquence. Ainsi, il suffit de mesurer le délai séparant l’arrivée du signal L1 de celle du signal L2, qui est proportionnel à l’erreur de temps due à la perturbation atmosphérique subie par les deux signaux. Retrancher l’intervalle trouvé au temps mesuré pour la réception du signal et multiplier ce dernier par la vitesse de la lumière permet finalement d’obtenir une distance satellite/récepteur corrigée.
d) Le positionnement relatif Lorsque le repérage n’a pas d’intérêt à être absolu, par exemple lors des mesures de mouvements tectoniques, l’étude des signaux enregistrés par deux récepteurs situés en 2 points différents mais peu éloignés (d’une distance maximale de 20 km) permet d’établir les variations du vecteur spatial reliant ces 2 points. En les considérant par rapport à un point de coordonnées connues dans le repère ECEF, on dispose d’une précision relative à ce point fixe de l’ordre du millimètre. Ce mode est d’ailleurs utilisé en géodésie, qui on le verra, est elle-même indispensable à la pertinence du positionnement absolu.
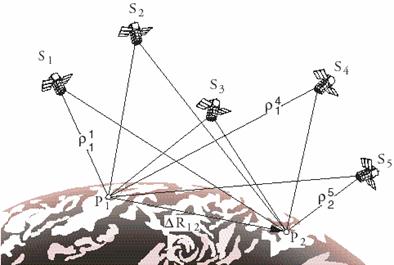
Mesure de positionnement relatif
d) La vitesse
Sans même mesurer la différence de position retranchée sur la différence de temps, il est possible de déterminer la vitesse du mobile récepteur par la simple prise en compte de l’effet Doppler sur les signaux. En effet, la fréquence porteuse du signal perçu par le récepteur GPS n’est plus exactement la même que celle générée par le satellite, car le rapport des fréquences dépend des vitesses relatives du satellite et de l'utilisateur. La vitesse du satellite étant facilement déterminable (à partir de l’information d’altitude de ses éphémérides et connaissant le rayon terrestre, il suffit d’appliquer la formule V=((Rayon de la Terre+Altitude) x 2p) / (période de révolution) ce qui donne une vitesse d’environ 3,8 km/s), la seule inconnue restante dans les formules relativistes de Doppler appliquées aux signaux électromagnétiques est la vitesse de l’utilisateur.
Une étude théorique du phénomène est disponible sur la page Internet de Michel Bonin, du C.E.R.E.S.P. de Dijon : http://www.ac-dijon.fr/pedago/Astronomie/AnalyseSpectrale/Doppler/Doppler.htm ou plus avancée, dans l’ouvrage La Nature sans foi ni loi de Christian Magnan, professeur au Collège de France dont la section consacrée à l’effet Doppler se trouve à cette adresse http://www.dstu.univ-montp2.fr/PERSO/magnan/doppler.html.
|


