|

|
|
|
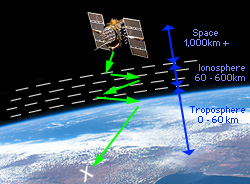
La modélisation de l'ionosphère, transmises aux satellites par les station de contrôle et incluse dans les bandes L1 et L2 permet au récepteur de corriger les données qu’il reçoit en fonction des conditions atmosphériques propre à sa situation géographique et à l'inclinaison du satellite sur l'horizon. Comme l'ionosphère est un milieu dispersif, la vitesse du signal la traversant dépend de la fréquence de l'onde radio. Les satellites émettant sur deux fréquences distinctes L1 et L2, certains récepteurs bifréquenciels peuvent éliminer l’erreur ionosphérique avec la technique dite de « mesure de phase », en corrélant l’écart d’arrivée des deux signaux à la perturbation dispersive. Jouxtant la Terre, la troposphère est quant à elle le lieu privilégié d’une réfraction des signaux. Cette couche s'élève à une altitude d'environ 11 km au-dessus des pôles et peut atteindre jusqu'à 16 km au-dessus des régions équatoriales. A fortiori, il est possible de la modéliser jusqu’à 60 km d’altitude. La durée de propagation de l'onde du signal satellitaire est affectée par la teneur en vapeur d'eau de cette couche basse de l'atmosphère, qui réfracte les ondes radios. Pour établir les imprécisions sur les mesures de pseudo-distances qui en découlent, il serait nécessaire de connaître cette quantité tout le long du trajet suivi par l'onde. En pratique cela se révèle très difficile, sinon impossible, même avec une mesure de phase utilisant les ondes L1 et L2 comme on peut le pratiquer pour l'ionosphère. Le phénomène des trajets multiples altère également la mesure de position. En effet, les ondes radios émises par les satellites peuvent être l’objet de réflexions en milieu urbain par les hautes infrastructures, qui augmentent la distance du trajet satellite/récepteur et donc la durée de propagation du signal. Le récepteur calcule alors une distance faussée et commet finalement une erreur sur la position. A tout cela, on peut enfin ajouter l’erreur due au bruit qui affecte tout signal radio. En résumé, nous pouvons dresser un tableau des principaux facteurs d’erreurs sur l’exactitude du positionnement absolu :
On serait tenté de calculer le total des perturbations, pour obtenir un intervalle de temps entre 131 et 164 ns, correspondant à une précision de 39,5 à 49,3 m, mais dans la pratique, les différents facteurs se compensent plus ou moins, ce qui permet une précision jusqu’à 10 fois supérieure. Avec une mesure différentielle (DGPS), les conséquences des facteurs d’erreur sur le calcul sont évidemment moindres :
Pour la même raison que précédemment, il serait importun d’additionner les erreurs. Bien qu’un total d’imprécision d’1,5 mètre serait déjà remarquable, la compensation confère au DGPS une précision inférieure au mètre.
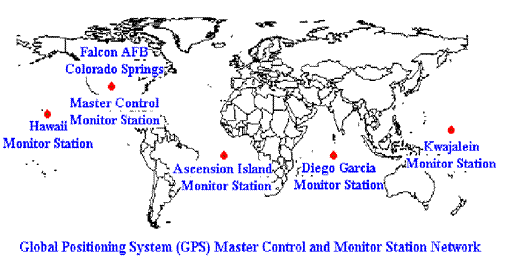
Cinq stations de surveillance coordonnées par la base militaire Falcon Air Force du Colorado (Etats-Unis) sont réparties autour de la planète afin que chaque satellite de la constellation GPS puisse être en permanence contrôlé par au moins une station. Leur mission est en effet de calculer l’orbite exacte des satellites et de leur transmettre incessamment les corrections nécessaires (éphémérides, synchronisation de leur horloge au temps UTC, dégradation des signal pour raison militaire). Ceci permet d’augmenter la fiabilité du système GPS en permettant à tout instant de vérifier que les informations générées par chacun des satellites sont correctes.
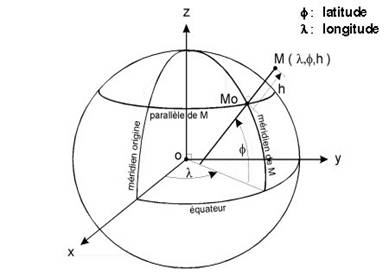
Le repérage théorique ECEF est séduisant, il n’empêche que la Terre est loin d’être une sphère parfaite! Sa surface topographique doit tenir compte des montagnes s’élevant à près de 9000 m d’altitude, des vallées et des fonds océaniques s’enfonçant à plus de 11000 m de profondeur. Au total, 20 km d’écart possible dont la tolérance ne serait pas seyante à une mesure GPS convenable. Une autre contrainte existe donc, indépendante des satellites, et néanmoins primordiale pour la justesse de la précision : la géodésie. Mais tout d’abord, un rappel des définitions des coordonnées d'un point en géographie fondamentale s’impose :
La géodésie est une science dont l’objectif est la modélisation de la forme et des dimensions de la Terre dans l'espace à trois dimensions. Jusqu’au XVIIème siècle, les savants admettant la sphéricité de la Terre n’avaient que le rayon de la Terre comme principale inconnue à résoudre. Seule la méthode des arcs était employée ; elle fut élaborée dans son principe par Eratosthène au III° siècle av. J. C., et met en oeuvre des mesures de distances à la surface de la terre et des mesures astronomiques, c'est-à-dire des mesures de directions de la verticale, pour un résultat final de seulement 3% d’erreur. Vous trouverezici un historique des principales méthodes utilisées pour la mesure de la Terre au cours des trois derniers millénaires. Il fut ensuite admis la difficulté d'une modélisation mathématique, bien qu’un ellipsoïde de révolution, aplati aux pôles, semblait constituer la meilleure approximation. C’est finalement en 1956 à Munich que le géodésien anglais Hotine présente la géodésie tridimensionnelle. Il ne s’agit plus de considérer l'espace à deux dimensions de la surface d'un ellipsoïde de référence, dimensions auxquelles on ajoute l'altitude, mais un système directement à trois dimensions défini par un trièdre trirectangulaire de coordonnées, et par un certain nombre de trièdres auxiliaires locaux rattachés à ce dernier. Les paramètres d’un point de la surface topographique sont ainsi ses coordonnées spatiales (x,y,z). La géodésie vise alors à décrire directement la forme de la surface topographique, sans chercher à lui imposer a priori le support approché de l'ellipsoïde. A la description géométrique s'ajoute en outre une description dynamique : le potentiel et la pesanteur en chaque point qui permettra d’établir une synthèse à travers la modélisation informatique du géoïde terrestre.
Une telle représentation s’impose pour la pertinence des données de repérage satellitaire car tout système de coordonnées repose sur une définition de paramètres cartographiques issus de la géodésie et de la physique. Pour le système GPS, on a défini une référence globale répondant aux objectifs d'un système mondial de navigation : en 1972 est créé la norme WGS72 (World Geodetic System 1972) qui deviendra WGS84 (World Geodetic System 84) douze ans plus tard. Le système est défini par un repère géocentrique de coordonnées cartésiennes (x,y,z) et d’origine le centre de gravité de la Terre. L'axe z passe par l'axe de rotation de la Terre et l'axe x est l'intersection de l'équateur avec le méridien de Greenwich. La surface ainsi déterminée est équipotentielle au champ de gravité terrestre, et coïncide avec le niveau moyen des mers. Cette surface est donc en tout point perpendiculaire à la direction indiquée par un fil à plomb (verticale du lieu). Les conversions de systèmes géodésiques nécessitent ainsi sept paramètres de conversions : 3 paramètres de translation, 3 paramètres de rotation, et un paramètre de facteur d’échelle. Une fois la position repérée dans un système géodésique, elle est transmise à l’utilisateur sous la principale forme : longitude, latitude, ou bien dans un nouveau système qui est de plus en plus fréquemment utilisé : le système UTM (Universal Transverse Mercator). Celui-ci fut créé de manières à éviter les problèmes de conversion entre degrés et mètre. Il se base sur une décomposition de la Terre en 60 fuseaux de 6° chacun, numérotés de 01 à 60, et de 20 bandes de 8° chacune, identifiées par des lettres : cliquez ici pour visualiser le découpage. La France est ainsi située dans les zones 30U, 31U, 32U, 30T, 31T, 32T. Une correction préétablie en fonction de la zone du récepteur étant systématiquement apportée, ce système permet de ne pas ralentir les calculs de distance.
|